Learning Multiplication: 6.2 x 0.1 Explained

Multiplication is one of the fundamental mathematical operations that forms the backbone of various real-world calculations. Understanding the principles behind multiplying numbers, particularly decimals like 6.2 and 0.1, is essential for mastering this operation. Let’s dive into an in-depth exploration of this concept and break it down step by step to build a strong foundation in decimal multiplication.

What Does Multiplying 6.2 by 0.1 Mean?

Multiplication, at its core, is a repeated addition process. However, when decimals are involved, it shifts to representing fractions or parts of whole numbers. Multiplying 6.2 by 0.1 means we are calculating one-tenth of 6.2. Essentially, we are determining what a small fraction of 6.2 would be when it is divided into ten equal parts.

Understanding Decimal Multiplication

To understand the multiplication of decimals like 6.2 and 0.1, we must first revisit how decimals work. A decimal number consists of two parts separated by a decimal point: the whole number part and the fractional part. Here’s what happens during multiplication:

1. Ignore the Decimal Points Initially
   Treat the numbers as whole numbers for the first step. For example, consider 62 (from 6.2) and 1 (from 0.1). Multiply them as you normally would.
2. Account for Decimal Places
   After performing the multiplication, count the total number of decimal places from the original numbers. In this case:
   • 6.2 has one decimal place.
   • 0.1 also has one decimal place.
     Together, they make two decimal places.
3. Adjust the Product
   Place the decimal point in the product such that it has the correct number of decimal places.

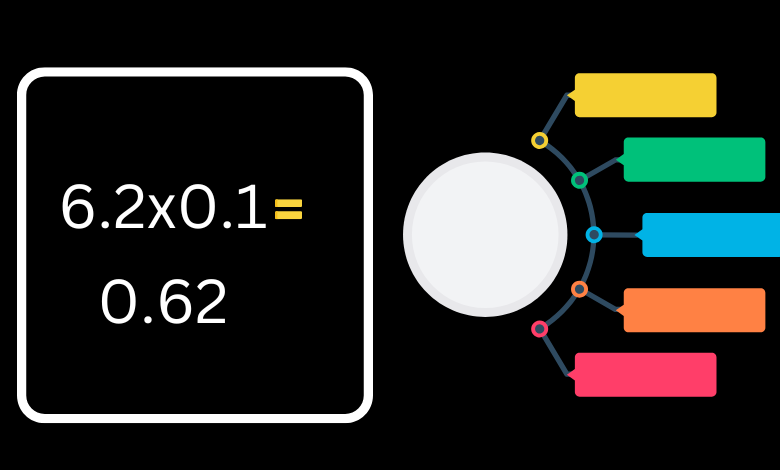
Using this method, 6.2 × 0.1 becomes 0.62.

Step-by-Step Calculation of 6.2 x 0.1

Step 1: Remove Decimals Temporarily

Write the numbers without decimals:

• 6.2 becomes 62.
• 0.1 becomes 1.

Step 2: Multiply the Whole Numbers

Now, multiply 62 by 1:
$62\times 1=62$

Step 3: Count Decimal Places

Count the decimal places in the original numbers:

• 6.2 has 1 decimal place.
• 0.1 has 1 decimal place.
  Thus, the product must have 2 decimal places.

Step 4: Place the Decimal Point

Insert the decimal point into the product (62) so that it has 2 decimal places:
$62\to 0.62$

Thus, the result of 6.2 × 0.1 is 0.62.

Common Misconceptions in Decimal Multiplication

Many learners struggle with decimal multiplication due to the placement of the decimal point. Here are a few tips to avoid common errors:

• Forget Counting Decimal Places: Always ensure you account for the correct number of decimal places in the final product.
• Treat Decimals Like Fractions: Remember, decimals are fractions in disguise. For instance, 0.1 is equivalent to 110\frac{1}{10}101​, and multiplying by 0.1 is like dividing by 10.
• Practice Simplification: Use simpler numbers or mental math techniques to verify results.

Real-Life Applications of Multiplying Decimals

Decimal multiplication has numerous applications, including:

1. Financial Calculations
   Understanding decimal multiplication is essential for computing interest rates, taxes, and discounts. For instance, calculating 10% of $6.20 requires multiplying 6.2 by 0.1, resulting in $0.62.
2. Measurement Conversions
   Decimals are commonly used in unit conversions, such as converting meters to kilometers or ounces to pounds.
3. Scientific Computations
   In fields like physics and chemistry, precise decimal calculations are crucial for determining quantities, rates, and proportions.
4. Everyday Shopping
   Decimal multiplication comes into play when calculating totals, splitting bills, or evaluating prices.

Tips to Master Decimal Multiplication

1. Practice Mental Math
   Familiarize yourself with simple decimal multiplications, like 0.1 × 5 or 0.25 × 4. This will help you develop a deeper intuition for the operation.
2. Break Down Complex Problems
   Divide the problem into smaller steps, focusing first on the whole numbers before reintroducing the decimals.
3. Use Estimation for Verification
   Estimate the product beforehand to check if your answer is reasonable. For example, multiplying a number by 0.1 will always make it ten times smaller.
4. Work on Word Problems
   Solve practical word problems involving decimals to enhance your real-world application skills.

Conclusion

Multiplying decimals like 6.2 and 0.1 may seem challenging at first, but with the right approach and understanding, it becomes a straightforward process. By following the step-by-step calculation method outlined above, you can confidently multiply any decimal numbers. Remember, the key lies in understanding the relationship between decimals and fractions, keeping track of decimal places, and practicing regularly. Whether for academic purposes, daily tasks, or professional calculations, mastering decimal multiplication is an invaluable skill.