Mpm2d rosedale unit 1: A Comprehensive Overview
Introduction
The MPM2D Rosedale Unit 1 provides an essential foundation for Grade 10 mathematics students, focusing primarily on linear systems and relations. This unit helps learners understand the principles of algebra and geometry, equipping them with the skills needed for advanced mathematical concepts. In this article, we will explore the core topics, learning objectives, and practical applications that make Unit 1 a critical component of the MPM2D curriculum.
Understanding Linear Relations
Linear relations form the cornerstone of Unit 1, introducing students to the concept of relationships between variables. A linear relation is defined as a relationship that can be represented graphically by a straight line on a Cartesian plane. This section delves into the key characteristics of linear relations, including slope, y-intercept, and the general form of a linear equation.
Students learn to derive and interpret the slope (‘m’) as the rate of change, which represents how one variable changes concerning another. For instance, in real-world scenarios like speed versus time or cost versus quantity, linear relations provide a simplified model for understanding trends and predicting outcomes. Additionally, the y-intercept (‘b’) highlights where the line crosses the vertical axis, offering a point of reference in problem-solving.
Graphing Linear Equations
Graphing is a fundamental skill emphasized in Unit 1. Students practice plotting linear equations by identifying points or using the slope-intercept form (‘y = mx + b’). Accuracy and precision are crucial in creating graphs that effectively illustrate relationships.
This topic also introduces students to different types of slopes: positive, negative, zero, and undefined. For example, a positive slope indicates an upward trend, such as an increase in temperature over time, while a negative slope represents a downward trend, such as a decrease in expenses. Through hands-on graphing exercises, students develop a deeper understanding of how changes in slope and intercept affect the overall representation of linear relations.
Introduction to Linear Systems
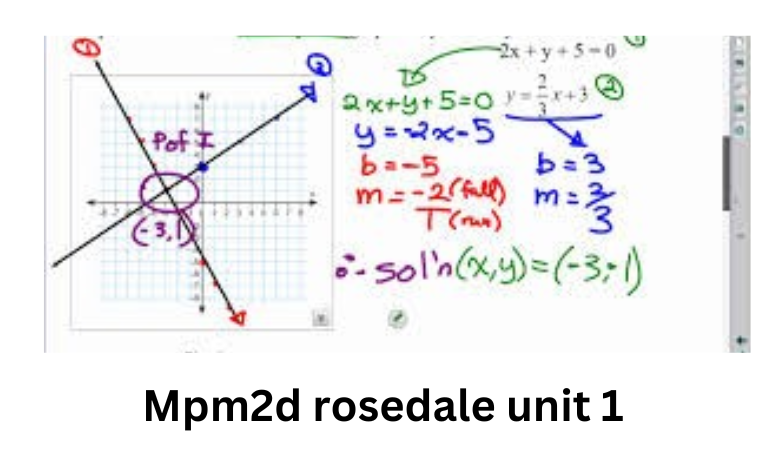
Linear systems consist of two or more linear equations that share a common solution. This section introduces students to the idea of solving systems algebraically and graphically. The solution to a linear system is the point of intersection between two lines on a graph, representing the values that satisfy both equations simultaneously.
For instance, in a system with the equations ‘y = 2x + 3’ and ‘y = -x + 5,’ the intersection point represents the values of ‘x’ and ‘y’ that fulfill both conditions. Students learn to analyze and interpret these solutions in various contexts, such as determining equilibrium points in economics or balancing chemical equations in science.
Methods for Solving Linear Systems
Unit 1 emphasizes three primary methods for solving linear systems:
- Graphical Method: Plotting equations on a graph and identifying the intersection point. This visual approach helps students understand the relationship between equations but may lack precision for complex problems.
- Substitution Method: Solving one equation for a variable and substituting the result into the other equation. This method is particularly effective for systems with straightforward equations.
- Elimination Method: Adding or subtracting equations to eliminate a variable, simplifying the system into a single equation. This technique is powerful for solving systems algebraically and is often used in advanced applications.
By practicing these methods, students develop flexibility and confidence in approaching linear systems from multiple angles, preparing them for diverse problem-solving scenarios.
Real-World Applications of Linear Systems
Understanding linear systems is not limited to academic exercises; it has practical applications across various fields. For example:
- Business and Finance: Determining the break-even point, where revenue equals expenses, is a direct application of linear systems.
- Engineering: Balancing forces in mechanical systems often involves solving linear equations.
- Environmental Science: Predicting population growth or resource depletion over time can be modeled using linear relations.
These applications demonstrate the relevance of linear systems in everyday life and professional settings, reinforcing their importance in the curriculum.
Tips for Success in Unit 1
- Master the Basics: Ensure a strong grasp of slope, intercept, and graphing techniques, as these skills are foundational for more complex topics.
- Practice Regularly: Frequent practice with linear equations and systems enhances problem-solving speed and accuracy.
- Apply to Real-World Problems: Connect mathematical concepts to practical scenarios to deepen understanding and retention.
- Seek Help When Needed: Collaborate with peers, ask questions in class, and use online resources to clarify doubts and strengthen comprehension.
Conclusion
The MPM2D Rosedale Unit 1 serves as a critical stepping stone for students’ mathematical journeys, offering essential skills in linear relations and systems. By mastering these concepts, students build a robust foundation for advanced topics in algebra, calculus, and beyond. Emphasizing both theoretical understanding and practical application, Unit 1 ensures that learners are well-equipped to tackle challenges in academics and real-world contexts.



